W naszym potocznym rozumieniu chaos to co┬ niedobrego; co┬Â, na co raczej nie czekamy - wi├¬cej: przera┬┐a nas my┬Âl o spo┬│ecznym chaosie, o chaotycznie pracuj┬▒cej elektrowni atomowej itd. Chcieliby┬Âmy mie├Ž ┬Âwiat i wyobra┬┐enie o nim uporz┬▒dkowane, sta┬│e i niezmienne.
Lecz dzisiaj tego typu "jednoznaczne" teoria, za┬│o┬┐enia i wynikaj┬▒ce ze├▒ "pewniki" zostaj┬▒ bardzo powa┬┐nie poddane w w┬▒tpliwo┬Â├Ž. Pow├│d? Przemo┬┐ny wp┬│yw (naturalnie nie zawsze przecie┬┐ u┬Âwiadamiany) Teorii Chaosu. Dzisiejsza nauka, zwana te┬┐ „now┬▒ nauk┬▒”, odchodzi i przekracza dotychczasow┬▒ wiedz├¬ wraz z jej tradycyjnymi aksjomatami i porusza si├¬ po obszarach, kt├│re laikowi wydawa├Ž si├¬ musz┬▒ "paranormalne". Naukowcy te┬┐ maj┬▒ swe przekonania, lecz trudno je nazwa├Ž wiar┬▒ - trudno w co┬ wierzy├Ž, gdy si├¬ to wie... Teoria Chaosu - kt├│ra opiera si├¬ na za┬│o┬┐eniu, i┬┐ mo┬┐liwe jest dokonywanie pomiar├│w, kontrolowanie lub odtwarzanie matematycznie nieprzewidywalnego zachowania si├¬ uk┬│ad├│w lub przebiegu zjawisk (procesy chaotyczne mo┬┐na zaobserwowa├Ž np. w przebiegu zjawisk atmosferycznych b┬▒d┬╝ w turbulencjach ruchliwych cieczy, kiedy to ledwie dostrzegalne zak┬│├│cenia warunk├│w pocz┬▒tkowych powoduj┬▒ znacz┬▒ce zmiany w ko├▒cowych stadiach ruchu; istnieje poetyczna wizja motylego skrzyd┬│a, kt├│re wprawione w ruch w Afryce wp┬│ywa na przebieg globalnych zjawisk klimatycznych) - po prostu dezaktualizuje wi├¬kszo┬Â├Ž naszych dotychczasowych pogl┬▒d├│w, przekona├▒ i tradycyjnych wiar zbudowanych na starych paradygmatach, zupe┬│nie nieprzystawalnych jako narz├¬dzia do dzisiejszych problem├│w, potrzeb, pyta├▒ i odkry├Ž.
Dlaczego tak si├¬ dzieje? Co si├¬ sta┬│o? Ot├│┬┐ "odpowiedzialne" s┬▒ tu pospo┬│u: fizyka kwantowa, relatywizm nauki, zasada nieokre┬Âlono┬Âci Wernera Heisenberga (teoria m├│wi┬▒ca, i┬┐ obserwacja danego procesu nieuchronnie oddzia┬│uje na ten proces, a zatem wyniki takiej obserwacji s┬▒ zawsze warto┬Âciami relatywnymi, nie absolutnymi), zasada antropiczna (zesp├│┬│ teorii fizycznych i kosmologicznych g┬│osz┬▒cych, ┬┐e obecno┬Â├Ž cz┬│owieka (gr. anthropos) we wszech┬Âwiecie nie jest przypadkowa, a cz┬│owiek jako obserwator kosmosu jest czynnikiem determinuj┬▒cym prawdopodobie├▒stwo w fizyce, ma on te┬┐ zasadniczy wp┬│yw na powstawanie rozmaitych zjawisk we wszech┬Âwiecie, przetwarza i przekazuje informacje, co by┬│oby potwierdzeniem Einsteinowskiej koncepcji czasoprzestrzeni), a tak┬┐e wynikaj┬▒ca z tego wszystkiego "nowa kosmologia".
Dokonuj┬▒c analizy wy┬│┬▒cznie na bazie fizyki (szczeg├│lnie dynamiki) rozr├│┬┐niamy trzy mo┬┐liwe typy zachowa├▒ uk┬│ad├│w dynamicznych: periodyczne (w┬│┬▒czaj┬▒c tu niezale┬┐ne od czasu), quasiperiodyczne i chaotyczne. Zachowanie quasiperiodyczne jest z┬│o┬┐eniem przebieg├│w periodycznych o niewsp├│┬│miernych cz├¬sto┬Âciach.
Zachowanie chaotyczne charakteryzuje si├¬ niestabilno┬Âci┬▒ (brakiem stanu r├│wnowagi, nie trwa┬│o┬Âci┬▒) rozwi┬▒za├▒ r├│wnania ruchu ze wzgl├¬du na warunki pocz┬▒tkowe. Oznacza to, ┬┐e dowolnie ma┬│a zmiana stanu pocz┬▒tkowego prowadzi po jakim┬ czasie do jako┬Âciowych zmian trajektorii.
Chaos nie wystêpuje w uk³adach, opisanych liniowymi równaniami ruchu.
Do analizy uk┬│adu wykazuj┬▒cego charakter chaotyczny u┬┐ywa si├¬ specjalnie do tego zdefiniowanych poj├¬├Ž. Powy┬┐ej wspomnia┬│em o „czasie charakterystycznym”. C├│┬┐ to takiego? Uk┬│ad chaotyczny jak wiemy wzmacnia odchylenia pocz┬▒tkowe, wi├¬c czas charakterystyczny uk┬│adu jest okresem po kt├│rym odchylenie to wzrasta dziesi├¬ciokrotnie. Dwie trajektoria odleg┬│e na pocz┬▒tku o d b├¬d├¬ po up┬│ywie czasu charakterystycznego odleg┬│e o 10d. Drugim wa┬┐nym poj├¬ciem jest atraktor. Definiuje si├¬ go jako wyr├│┬┐niony podzbi├│r mo┬┐liwych stan├│w uk┬│adu do kt├│rego nieuchronnie zmierza ewolucja uk┬│adu. Najlepiej jednak to przestawi├Ž na przyk┬│adzie. Maj┬▒c do dyspozycji wahad┬│o, mocujemy je i puszczamy z dowolnego po┬│o┬┐enia. Wiemy, ┬┐e pod wp┬│ywem si┬│ tarcia (wahad┬│o o powietrze oraz w zamocowaniu) zatrzyma si├¬ w ko├▒cu po jakim┬ trudno przewidywalnym czasie. Wiadomo r├│wnie┬┐, ┬┐e ten stan jest nieunikniony tj. osi┬▒gni├¬cie w/w stanu nie jest zdeterminowane pr├¬dko┬Âci┬▒ pocz┬▒tkow┬▒ ani warto┬Âci┬▒ wychylenia. Tak, wi├¬c to spoczynkowe po┬│o┬┐enie wahad┬│a b├¬dzie dla tego uk┬│adu atraktorem. W powy┬┐szym przyk┬│adzie atraktorem b├¬dzie konkretny punkt spoczynkowy jednak bardzo cz├¬sto spotyka si├¬, ┬┐e atraktory o skomplikowanej strukturze. Szczeg├│ln┬▒ klas├¬ stanowi┬▒ atraktory dziwne. Odwo┬│uj┬▒c si├¬ do trajektorii mo┬┐na je zdefiniowa├Ž jako takie, kt├│re przyci┬▒gaj┬▒ trajektorie z zewn┬▒trz a ruch w ich wn├¬trzu jest chaotyczny i nieprzewidywalny. Bardzo s┬│awnym atraktorem rozbudzaj┬▒cym wyobra┬╝ni├¬ naukowc├│w od 1963r. (data publikacji) jest atraktor Lorenza. Jak ju┬┐ wcze┬Âniej wspomnia┬│em zajmowa┬│ on si├¬ metrologi┬▒ i post├¬puj┬▒c z duchem teorii chaosu uda┬│o mu si├¬ upro┬Âci├Ž bardzo skomplikowane r├│wnania opisuj┬▒ce zale┬┐no┬Âci bardzo du┬┐ej liczby zmiennych. Wynikiem jego prac s┬▒ (s┬│awne ju┬┐) trzy r├│wnania r├│┬┐niczkowe (ju┬┐ wspomniane). Pomimo, ┬┐e baz┬▒ by┬│y badania metrologiczne same r├│wnania przez znaczne uproszczenie uzyska┬│y pewien dystans od pierwotnych za┬│o┬┐e├▒. Tym nie mniej pozwoli┬│o to zobrazowa├Ž atraktor ju┬┐ na p┬│aszczy┬╝nie trzy wymiarowej.

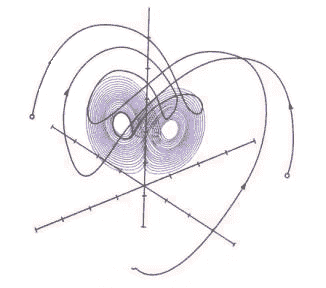
Poza „dziwnymi atraktorami” wyst├¬puj┬▒ te┬┐ atraktory samopodobne. W nich natomiast kszta┬│ty staj┬▒ si├¬ bardzo uporz┬▒dkowane i systematyczne. Doskona┬│ymi przyk┬│adami s┬▒ fraktale.
Fraktalami (┬│ac. fractus z┬│amany) nazywamy zbiory geometryczne, dla kt├│rych wymiar jest liczb┬▒ naturaln┬▒. Przyk┬│adowo, fraktalem o wymiarze r├│wnym stosunkowi logarytmu z 2 do logarytmu z 3 jest zbi├│r Cantora (podzbi├│r odcinka o wymiarze 1), a dywan Sierpinskiego (podzbi├│r kwadratu) stanowi fraktal o wymiarze ln8/ln3.
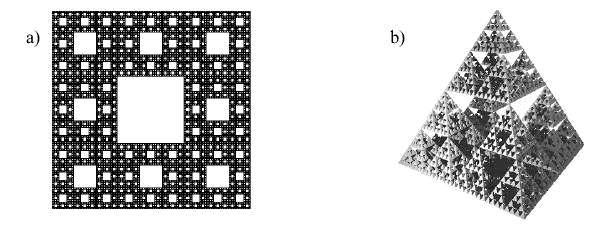
a) dywan Sierpi├▒skiego o wymiarze D = ln8/ln3; b) piramida Sierpi├▒skiego o wymiarze D = 2
Wiêcej znajdziesz tu:
http://www.fizykon.org/fiz_wspolczesna/teoria_chaosu.htm