Mówi¹c o wymiarze przestrzeni, myœlimy o trzech wzajemnie prostopad³ych wektorach, nie zwa¿aj¹c na to, ¿e fizycznoœÌ reperu trzech wektorów ma uzasadnienie jedynie w naszych warunkach ziemskich, gdzie Ziemia w swojej p³aszczyŸnie daje dwa z nich, a kierunek ciê¿aru trzeci. Jeœliby nam przysz³o rozwin¹Ì cywilizacjê w miejscu, gdzie brak grawitacji, sk¹d wziê³aby siê w naszym umyœle prostopad³oœÌ? Niech to pytanie bêdzie sygna³em w¹t³oœci naszych przes³anek co do wyboru konwencji matematycznych, które s¹ dalekie od uniwersalnoœci. Mimo to wymiarem, opartym na pojêciu reperu wzajemnie prostopad³ych wektorów, fizycy pos³uguj¹ siê nie tylko w makroœwiecie, ale i w mikroœwiecie, o którym ju¿ Riemann pisa³, ¿e zapewne rz¹dzi siê inn¹ geometri¹.
http://www.swietageometria.darmowefora.pl/index.php?topic=15.msg3717#msg37171.5 Cytaty
Platon
a) „Co do obrotĂłw innych planet, ludzie ich nie znajÂą, z wyjÂątkiem bardzo niewielu, i nie dajÂą im nazw ani nie mierzÂą za pomocÂą obserwacji ich stosunkĂłw do Liczb. ToteÂż nic — Âżeby tak powiedzieĂŚ — nie wiedzÂą, Âże i ich obroty, ktĂłrych jest nieskoĂączona iloœÌ i zadziwiajÂąca ró¿norodnoœÌ, mierzÂą czas. MoÂżna mimo to zrozumieĂŚ, Âże doskonaÂła liczba czasu wtedy wypeÂłnia rok doskonaÂły, gdy osiem obrotĂłw po wyrĂłwnaniu swych szybkoÂści powraca do punktu wyjÂścia — osiem obrotĂłw mierzonych wedÂług orbity Tego Samego, ktĂłre siĂŞ porusza w sposĂłb jednostajny”[236].
b) „CaÂły ten wszechÂświat raz sam BĂłg prowadzi w biegu i sam go obraca, a raz go zostawia, kiedy jego obroty juÂż osiÂągnÂą miarĂŞ czasu jemu wÂłaÂściwego. Wtedy siĂŞ wszechÂświat zaczyna sam krĂŞciĂŚ w stronĂŞ przeciwnÂą, bo on jest istotÂą ÂżywÂą i dostaÂł rozum od tego, ktĂłry wprowadziÂł weĂą harmoniĂŞ na poczÂątku. (...) nie trzeba mĂłwiĂŚ, ani Âże Âświat siĂŞ zawsze sam obraca, ani teÂż Âże BĂłg zawsze go obraca i w dwĂłch przeciwnych krĂŞci go kierunkach, ani teÂż Âże go krĂŞcÂą jacyÂś dwaj bogowie, sobie nawzajem przeciwni, tylko (...) to jedno pozostaje, Âże raz go prowadzi przyczyna inna, boska, i on wtedy znowu nabiera Âżycia i dostaje nieÂśmiertelnoœÌ nabytÂą od swego wykonawcy, a raz, kiedy go BĂłg opuÂści, on wtedy idzie sam przez siĂŞ, jak dÂługo jest zostawiony sam sobie. Tak, Âże z powrotem odbywa niezliczone obroty, bo jest czymÂś najwiĂŞkszym i najlepiej zrĂłwnowaÂżonym, i biegnie, oparty na osi najcieĂąszej. (...) ruch obrotowy Âświata odbywa siĂŞ raz w tym kierunku, co teraz, a raz w stronĂŞ przeciwnÂą. (...). TĂŞ przemianĂŞ trzeba uwaÂżaĂŚ za najwiĂŞkszÂą ze wszystkich przemian, jakie siĂŞ odbywajÂą, i najbardziej zasadniczÂą we wszechÂświecie”[237].
2.5 Komentarz
Czy istnieje potrzeba wprowadzania dziÂś modeli kosmologicznych z „pitagorejskim”, cyklicznym czasem? Aby odpowiedzieĂŚ na to pytanie przeÂśledÂźmy najpierw pokrĂłtce w jakim punkcie znajduje siĂŞ obecnie kosmologia ze wzglĂŞdu na moc eksplanacyjnÂą dotychczasowych jej modeli i ich zdolnoÂśc do tÂłumaczenia znanych w dniu dzisiejszym empirycznych zjawisk, mĂłwiÂących o budowie WszechÂświata jako caÂłoÂści. Otó¿, jak wiadomo, z rĂłwnaĂą OgĂłlnej Teorii WzglĂŞdnoÂści wynikajÂą — przy dodatkowym zaÂłoÂżeniu homogenicznoÂści oraz izotropowoÂści WszechÂświata — trzy moÂżliwe typy jego geometrii, ktĂłre byÂły tu schematycznie przedstawione na rysunku 5. Owe trzy typy geometrii WszechÂświata powiÂązane sÂą ÂściÂśle zarĂłwno z problemem wieku Kosmosu, jak i sposobem jego ewolucji. Zale¿¹ one, jak rĂłwnieÂż powszechnie wiadomo, od gĂŞstoÂści materii w universum Ω: dla gĂŞstoÂści mniejszej od tzw. GĂŞstoÂści krytycznej Ω0 otrzymujemy wszechÂświat hiperboliczny, dla wiĂŞkszej — sferyczny, dla gĂŞstoÂści krytycznej zaÂś [Ω = Ω0] — wszechÂświat pÂłaski.
Sferyczny model Wszechœwiata oznacza jego zamkniêtoœÌ (w czasie oraz w przestrzeni). Natomiast modele p³aski i hiperboliczny daj¹ jako ich konsekwencjê Wszechœwiat otwarty i byÌ mo¿e nieskoùczony.
W kaÂżdym razie, potwierdzone przez Roukeme et al. wnioski Weeksa i Lumineta skÂłaniajÂą do przyjĂŞcia jako adekwatnego do rzeczywistoÂści sferycznego modelu geometrii wszechÂświata. Tymczasem model ten uwaÂżaÂło siĂŞ dotÂąd raczej — w Âświetle obecnych obserwacji — za najmniej moÂżliwy [wzgl. najmniej prawdopodobny]. Jak pisaÂł o tym w 1998 roku A. Liddle: „Ci z nas, ktĂłrym podoba siĂŞ teoria inflacji, opowiadajÂą siĂŞ za modelem WszechÂświata pÂłaskiego. Niestety, coraz bardziej wyglÂąda na to, Âże aby mogÂło to byĂŚ prawdÂą, musimy raczej uwierzyĂŚ w istnienie staÂłej kosmologicznej, niÂż przyj¹Ì, Âże WszechÂświat ma po prostu gĂŞstoœÌ krytycznÂą. Hiperboliczny (otwarty) model WszechÂświata jest, oczywiÂście, nadal moÂżliwy, natomiast WszechÂświat o geometrii sferycznej (zamkniĂŞty) — bardzo maÂło prawdopodobny”[238].
Przeprowadzone od tego czasu obserwacje supernowych wskazujÂą natomiast na coraz szybsze tempo rozszerzania siĂŞ Kosmosu, a zatem wydawaÂły siĂŞ tym bardziej ÂświadczyĂŚ przeciwko modelowi sferycznemu[239]. WstĂŞpne bowiem wyniki obserwacji teleskopem Hubble’a supernowych z wysokim przesuniĂŞciem ku czerwieni zdawaÂły siĂŞ wskazywaĂŚ na pÂłaski — choĂŚ zarazem obecnie akcelerujÂący — model rozszerzajÂącego siĂŞ WszechÂświata. RĂłwnieÂż dane ze stratosferycznej sondy balonowej BOOMERANG zdawaÂły siĂŞ sugerowaĂŚ poprawnoœÌ pÂłaskiego modelu WszechÂświata. Najnowsze wyniki obserwacji mikrofalowego promieniowania tÂła sugerujÂą tymczasem wartoœÌ gĂŞstoÂści materii WszechÂświata w przedziale pomiĂŞdzy 1.00 a 1.04 gĂŞstoÂści krytycznej[240]. UprawdopodobniaÂło by to model sferyczny (lub ew. pÂłaski). Istotnie — jak juÂż pisaliÂśmy w A1 — najnowszy model WszechÂświata opracowany przez zespó³ Jeffreya Weeksa i Jean-Pierre Lumineta w oparciu o wyniki promieniowania tÂła podane przez sondĂŞ WMAP posÂługuje siĂŞ dodekahedralnÂą przestrzeniÂą PoincarĂŠgo, tzn. sytuuje siĂŞ w kaÂżdym bÂądÂź razie w rodzinie modeli sferycznych.
Dodekahedralny WszechÂświat Lumineta i Weeksa jest podwĂłjnie ikosahedralnÂą rozmaitoÂściÂą ró¿niczkowÂą rzĂŞdu 120, ktĂłrej podstawowÂą domenÂą jest dodekahedr[241]. Model Ăłw bardzo dobrze zgadza siĂŞ z wieloma danymi przesÂłanymi przez sondĂŞ WMAP, istnieje jednak rĂłwnieÂż inna propozycja interpretacji owych danych, dopasowujÂąca je do pÂłaskiego WszechÂświata[242]. Przedstawia jÂą zespó³ Davida Spergla z Princeton University: „However, in response to Weeks's report, Spergel and his colleagues have announced evidence that contradicts the findings. They showed previously that if the Universe does produce a hall-of-mirrors effect, it should be possible to find a pattern of matching circles in the microwave background around which the fluctuations are identical (New Scientist print edition, 19 September 1998, p 28). Weeks's theory predicts six specific pairs of matching circles in the sky, but Spergel's team has had no luck finding them in WMAP data. "Weeks's team has a very powerful model that's nice because it makes a very specific prediction about the pattern we should see on the sky," says Spergel. 'However, we've looked for it, and we don't see it' [243].
Ostatnio wszak¿e polsko-francuski zespó³ naukowy w opracowanych przez siebie wynikach uzyskanych z sondy WMAP potwierdzi³ model Weeksa i Lumineta, wyjaœniaj¹c zarazem negatywny wynik zespo³u Spergela, jako spowodowany faktem, i¿ Wszechœwiat znajduje siê dopiero na etapie wyewoluowania siê pojedynczego [stanowi¹cego zatem obecnie prawie ca³¹ objêtoœÌ universum] dodekahedru, przez co przewidywane w tym modelu teoretyczne zjawiska odbiÌ w promieniowaniu t³a s¹ jeszcze b. s³abe[244].
NaleÂżaÂłoby w tym miejscu podnieœÌ rĂłwnieÂż jednak fakt, iÂż nie tylko dodekahedralny, ale wszelkie modele sferyczne (z racji tego, iÂż sferyczny WszechÂświat dziaÂłaĂŚ by musiaÂł jak skupiajÂąca soczewka) przewidujÂą istnienie na niebie tzw. obrazĂłw-widm (ghost images) takich obiektĂłw jak np. galaktyki czy kwazary[245]. W sferycznym WszechÂświecie powinny wystĂŞpowaĂŚ obrazy-widma wszelkich w zasadzie obiektĂłw [ÂściÂśle rzecz biorÂąc efekt ten moÂże wystÂąpiĂŚ rĂłwnieÂż — choĂŚ w mniejszym na ogó³ natĂŞÂżeniu — takÂże w nie-sferycznym universum]. W zaleÂżnoÂści od szczegó³owej topologii takiego universum owe ghost images mogÂłyby byĂŚ b. liczne (nawet nieskoĂączenie liczne) i mogÂłyby dawaĂŚ tzw. efekt sali lustrzanej[246]. Mimo jednak podejmowanych juÂż od przedwojny licznych prĂłb[247], do tej pory takowych obrazĂłw nie udaÂło siĂŞ (przynajmniej jednoznacznie) zaobserwowaĂŚ[248]. ByĂŚ moÂże wszakÂże ostatni wynik polsko-francuskiego zespoÂłu tÂłumaczy rĂłwnieÂż ten fakt.
Mamy zatem obecnie w kosmologii do czynienia z “dramatycznym rozdarciem” pomiĂŞdzy dwoma konkurencyjnymi modelami (a raczej grupami modeli) wszechÂświata z jednej strony pÂłaskiego, z drugiej zaÂś — sferycznego. Jak wyÂżej pokazaliÂśmy, istniejÂą silne argumenty obserwacyjne (w³¹cznie z ‘dodekahedralnym’ materiaÂłem zinterpretowanym tu po raz pierwszy przez nas) ÂświadczÂące za kaÂżdÂą z tych opcji. Nie od rzeczy byÂłoby w takim razie przypuÂściĂŚ, iÂż moÂże — wedle zasady, Âże ‘prawda leÂży poÂśrodku’ — obydwa owe modele sÂą w jakimÂś stopniu adekwatne do fizycznej rzeczywistoÂści. Istotnie, gdyby odrzuciĂŚ klasycznÂą KopernikaĂąskÂą ZasadĂŞ KosmologicznÂą, tj. aprioryczne zaÂłoÂżenie o homogenicznoÂści i izotropowoÂści przestrzennej WszechÂświata, moglibyÂśmy wprowadziĂŚ jako Jego model np. powierzchniĂŞ 4-wymiarowego toroidu rogowego, ktĂłrego 3-wymiarowÂą reprezentacjÂą jest zwykÂły torus rogowy. Model taki byÂłby geometrycznie poÂśredni pomiĂŞdzy powierzchniÂą 4-wymiarowej hipersfery, reprezentujÂącej sferycznÂą geometriĂŞ Kosmosu, a powierzchniÂą 4-wymiarowego torusa pierÂścieniowego, ktĂłra jest przykÂładem jednego z najbardziej popularnych ostatnio modeli pÂłaskich [por. rys.12].
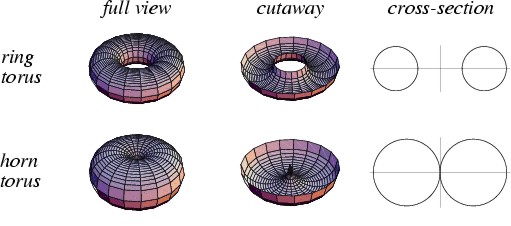
Rys. 12 Torus pierÂścieniowy (u gĂłry) jako rzut czterowymiarowego toroidu pÂłaskiej geometrii WszechÂświata oraz torus rogowy (u doÂłu) — przykÂład moÂżliwej „geometrii poÂśredniej” ktĂłra globalnie przypominaÂłaby geometriĂŞ sferycznÂą (180o < suma kÂątĂłw w trĂłjkÂącie < 540o), lokalnie zaÂś byÂłaby zbliÂżona do pÂłaskiej geometrii pierÂścieniowego torusa.
W naszym modelu ‘rogowym’ istnieje jeden punkt wyró¿niony (Âśrodek torusa rogowego), ktĂłry byÂłby tu modelem poczÂątkowego a zarazem koĂącowego punktu (propagacji) WszechÂświata. Czas jest w tym wypadku cykliczny (wszechÂświat zamkniĂŞty), co dobrze zgadza siĂŞ z naszymi ustaleniami nt. logicznie koniecznej natury czasu z poprzedniego paragrafu. W takim rogowym WszechÂświecie nie bĂŞdÂą wystĂŞpowaÂły w zasadzie (poza punktem poczÂątku-koĂąca) ghost images — takÂże w promieniowaniu tÂła — co z kolei dobrze zgadza siĂŞ z aktualnymi obserwacjami. Jednak taki WszechÂświat — jako ‘globalnie sferyczny’ — ‘rozpinany’ byÂłby przez (przestrzennÂą) siatkĂŞ dodekahedralnych geodetyk, co znowu stoi w zgodzie do przedstawionych przez nas rozumowaĂą i empirycznych danych.
W modelu tym jedynym peÂłnym obrazem-widmem byÂłby obraz-widmo punktu poczÂątkowego (osobliwego). Punkt ten zatem sam by siebie podwajaÂł [ogĂłlniej: multyplikowaÂł] — i w ten sposĂłb byÂłby ÂźrĂłdÂłem czasu. DopĂłki bowiem mamy do czynienia z jednym tylko punktem — jednÂą chwilÂą — nie moÂże istnieĂŚ ruch. Istnieje wĂłwczas tylko (statyczna) wiecznoœÌ. Czas zaÂś jest ex definitione „podwajaniem siĂŞ”, multyplikacjÂą (punktĂłw i chwil).
Natomiast fakt, iÂż (caÂły) czas wszechÂświata musi byĂŚ skoĂączony jest logicznie konieczny. RozwaÂżmy albowiem, co nastĂŞpuje. WeÂźmy dowolnÂą miarĂŞ (tj. jednostkĂŞ) czasu. Niech to bĂŞdzie — dla ustalenia uwagi — sekunda. Otó¿ sekunda jest (jednÂą) szeœÌdziesiÂątÂą czĂŞÂściÂą minuty, (jednÂą) 3600-tnÂą czĂŞÂściÂą godziny etc. Ale, w wypadku istnienia czasu nieskoĂączonego, sekunda byÂłaby 1/∞ — tj. [przy przejÂściu przez granice] dokÂładnie zerowÂą! — czĂŞÂściÂą takiego czasu (czasu w ogĂłle, czasu jako takiego). Gdyby jednak sekunda byÂła zerowÂą (tj. ÂżadnÂą) czĂŞÂściÂą czasu w ogĂłle, to wĂłwczas nie byÂłaby ona w ogĂłle czĂŞÂściÂą czasu. Nie bĂŞdÂąc zaÂś w ogĂłle [ÂżadnÂą] czĂŞÂściÂą czasu nie mierzyÂłaby go przeto. Innymi wiĂŞc sÂłowy, gdyby czas byÂł nieskoĂączony, byÂłby on wĂłwczas bezmierny — czyli byÂłby czasem bez miary, czasem pozbawionym miary. Nie moÂżna by byÂło go przeto mierzyĂŚ. A skoro czas daje siĂŞ jednak mierzyĂŚ, to musi byĂŚ on przeto skoĂączony, tj. okreÂślony (ograniczony kresem). Warto w tym miejscu odnotowaĂŚ, iÂż powyÂższe rozumowania wystĂŞpujÂą rzecz jasna przeciwko faktycznemu (tj. realnemu) istnieniu wszelkich zbiorĂłw nieskoĂączonych, przeciw istnieniu to ktĂłrych (np. przeciw nieskoĂączonej podzielnoÂści odcinka) wystĂŞpowaÂł juÂż m.in. wielokrotnie cytowany tu przez nas G.W. Leibniz[249].
W powyÂższym modelu mamy wiĂŞc do czynienia z czasem WszechÂświata cyklicznym, zamkniĂŞtym — caÂły WszechÂświat jest zaÂś periodyczny i pulsujÂący [takÂże periodycznÂą jest zarazem wskutek tego przestrzeĂą, ale fakt Ăłw jest rĂłwnieÂż logicznie konieczny — przestrzeĂą musi byĂŚ skoĂączona i periodyczna z tych samych wzglĂŞdĂłw, z ktĂłrych te wÂłaÂśnie cechy posiadaĂŚ winien czas]. Model czasu WszechÂświata pulsujÂącego [wzgl. periodycznego], czyli teÂż cyklicznego pojawia siĂŞ zresztÂą (rĂłwnieÂż cyklicznie i periodycznie) od momentu stworzenia pierwszego tego rodzaju modelu przez R.C. Tolmana [por. rys. 13] co jakiÂś [nomen atque omen] czas w kosmologii. MoÂże to ÂświadczyĂŚ za tym, iÂż tego rodzaju intuicja czasu (i) WszechÂświata jest (rĂłwnieÂż w nauce) g³êboko zakorzeniona[250].

Rys. 13 Kosmologiczny model Tolmana [za: M. Heller, 1983]. Jak pisze M. Heller: „Tolman wraz ze swoim wspó³pracownikiem Morganem Wardem wykazali, Âże jeÂżeli w modelu oscylujÂącym zachodzÂą procesy nieodwracalne, to okres trwania poszczegĂłlnych cykli wydÂłuÂża siĂŞ, a ich amplituda roÂśnie [...], w fazie rozszerzania siĂŞ WszechÂświata entropia wzrasta, w fazie kurczenia siĂŞ maleje, ale w kolejnych maksimach ekspansji entropia jest coraz wiĂŞksza. W ten sposĂłb WszechÂświat moÂże oscylowaĂŚ nieograniczenie. JednakÂże problem przejÂścia przez osobliwoÂści nadal pozostaje nierozwiÂązany. Tolman na wszelki wypadek na wykresie pozostawiÂł luki, nie narysowaÂł, jak sobie te przejÂścia wyobraÂża” [op. cit., s. 112-113].
Ponadto, przedstawiony tu przez nas model WszechÂświata byÂł zasadniczo juÂż od samego poczÂątku logicznie konieczny, tj. koniecznie prawdziwy. To wÂłaÂśnie tak naprawdĂŞ nic innego, a jedynie powierzchnia 4-wymiarowego toroidu rogowego, moÂże byĂŚ poprawnym modelem, otrzymanym jako odpowiedÂź na pytanie o (czaso-)przestrzenny ksztaÂłt Kosmosu. JeÂżeli pytamy bowiem w jakim ksztaÂłcie zamyka siĂŞ WszechÂświat w ogĂłle, to w odpowiedzi nie moÂżemy — logicznie rzecz biorÂąc — wymieniĂŚ Âżadnych szczegó³ów tegoÂż ksztaÂłtu: to, co jest tylko w ogĂłle, nie jest w Âżadnym szczegĂłle, nie moÂże byĂŚ niczym szczegó³owym. Dlatego teÂż najogĂłlniej rozumianym ksztaÂłtem Universum musiaÂłby byĂŚ ksztaÂłt doskonale homogeniczny i izotropowy, co implikuje — jako odpowiedÂź na tak ogĂłlne pytanie — ksztaÂłt ‘idealnej’ [tyle, Âże 4-wymiarowej] Parmenidejskiej kuli[251] [scil. 3-wymiarowej powierzchni hipersfery]. KaÂżda odpowiedÂź jest po prostu juÂż logicznie zawarta w [poprawnie zadanym] pytaniu. Z zadania sobie tegoÂż pytania o najogĂłlniej rozumiany charakter ksztaÂłtu WszechÂświata, wynika odpowiedÂź w postaci zasady kosmologicznej, gÂłoszÂącej homogenicznoœÌ i izotropowoœÌ Kosmosu[252]. Problem polega wszak na tym, Âże kiedy pytamy o czasoprzestrzenne granice Universum, to zadajemy w istocie pytanie juÂż nie o ten najbardziej ogĂłlnie rozumiany ksztaÂłt WszechÂświata, ale pytamy o czasowe granice przestrzennych granic i — tym samym — wchodzimy juÂż na poziom wiĂŞkszej (choĂŚ dopiero pierwotnej, tj. minimalnej) szczegó³owoÂści.
WeÂźmy zatem logicznie konieczny 2-wymiarowy model przestrzeni WszechÂświata. Musi nim byĂŚ — zgodnie ze wszystkim, co zostaÂło przed chwilÂą powiedziane — koÂło. JeÂżeli zadamy sobie teraz pytanie o czasowe granice tak rozumianego Universum (tj. czasowe granice universum rozpatrywanego na tym poziomie ogĂłlnoÂści, bÂądÂź szczegó³owoÂści), to otrzymamy w odpowiedzi — sytuujÂący siĂŞ gdzieÂś na tym kole (wyró¿niony) punkt [rys. 14].
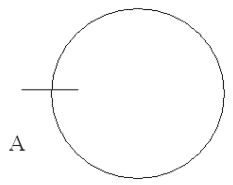
Rys. 14 Gdy fizycznÂą przestrzeĂą WszechÂświata przedstawimy w postaci (‘doskonaÂłego’) okrĂŞgu, wĂłwczas jej granica — czas — bĂŞdzie, naniesionym na Ăłw okrÂąg, punktem.
Tak, jak punkt jest bowiem granicÂą linii[253], tak i czas jest granicÂą, tj. zewnĂŞtrznym ksztaÂłtem a. formÂą przestrzeni. Jest tak po pierwsze dlatego, gdyÂż forma przestrzeni jest tejÂże przestrzeni strukturÂą, a wiĂŞc w tym wypadku [zadanÂą na owej przestrzeni] metrykÂą. Metryka zaÂś — lub mĂłwiÂąc po prostu odlegÂłoœÌ — zjawia siĂŞ w przestrzeni dopiero wraz z czasem. Gdyby nie byÂło czasu, pokonanie jakiejkolwiek odlegÂłoÂści nie trwaÂłoby nigdy dÂłuÂżej niÂż chwilĂŞ, przez co odlegÂłoÂści de facto nie istniaÂłyby, przez co z kolei wszystkie punkty przestrzeni naleÂżaÂłoby ze sobÂą utoÂżsamiĂŚ. W takim jednak wypadku przestrzeĂą — nie posiadajÂąc czĂŞÂści (sprowadzaÂłaby siĂŞ bowiem do punktu)[254] — nie miaÂłaby teÂż i [wewnĂŞtrznej] budowy, struktury. W drugÂą stronĂŞ zresztÂą rĂłwnieÂż i dystans przestrzenny implikuje swoim istnieniem czas. Czas albowiem — jako toÂżsamy z najogĂłlniej rozumianym ruchem[255] — wymaga dystansu dla swego istnienia. Przeto wiĂŞc dystans [przestrzenna odlegÂłoœÌ a. odlegÂłoœÌ w przestrzeni] i czas sÂą to pojĂŞcia rĂłwnozakresowe. [Metryczny] dystans [czas] jest wiĂŞc strukturÂą [ksztaÂłtem, granicÂą] przestrzeni.
Po drugie — czas jako spirala jest tworem pÂłaskim, 2-wymiarowym, przeto przystoi mu ograniczaĂŚ 3-wymiarowÂą przestrzeĂą[256].
Po trzecie przestrzeĂą fizyczna, ktĂłra jest z jej definicji najprostszym dajÂącym siĂŞ dostrzec zmysÂłowo tworem[257], wymaga jako swej antytezy (granicy) tego, co jest jeszcze niewidzialne (nie dajÂące siĂŞ dostrzec zmysÂłowo) a takÂą jest wÂłaÂśnie rzeczÂą czas.
NaleÂżaÂłoby tu tylko jeszcze zauwaÂżyĂŚ, iÂż czas — jako wÂłaÂśnie graniczna [tj. skrajna] forma przestrzeni, naleÂży do tej przestrzeni, zawiera siĂŞ w niej — nie moÂże stanowiĂŚ on przeto odrĂŞbnego, „czwartego” wymiaru.
W kaÂżdym razie, na owym jednowymiarowym, liniowym [w postaci okrĂŞgu] modelu przestrzeni trĂłjwymiarowej, czas bĂŞdzie wiĂŞc punktem. Gdy uwzglĂŞdniamy czas w przestrzeni — wyró¿niamy na tej linii punkt. JeÂśli chcemy zaÂś przejœÌ do przestrzeni trĂłjwymiarowej, zrealizowaĂŚ zatem model (speÂłniĂŚ go), musimy obrĂłciĂŚ rzecz jasna caÂły model [aÂżeby staÂł siĂŞ peÂłnym] wokó³ punktu-czasu najpierw w przestrzeni 3-, potem zaÂś 4-wymiarowej, otrzymujÂąc [kolejno] torus rogowy, oraz 4-wymiarowy rogowy hipertoroid. Wyró¿niony albowiem na kole przestrzennym punkt czasu stanowi formĂŞ, tj. granicĂŞ owej przestrzeni. ÂŻeby jednakÂże urzeczywistniĂŚ Ăłw model, trzeba go zrealizowaĂŚ, tzn. speÂłniĂŚ. SpeÂłnienie zaÂś czegoÂś jest (jego) obrotem, obrĂłceniem, tj. takÂże — odwrĂłceniem [a wiĂŞc — w tym wypadku — zamienieniem formy i treÂści; treœÌ koÂła przestrzeni staĂŚ siĂŞ musi a zatem formÂą otaczajÂącÂą znajdujÂącÂą siĂŞ tym razem wewnÂątrz treœÌ czasu-formy — i stÂąd siĂŞ bierze charakter ww. obrotu].
WĂłwczas otrzymamy rzecz jasna model WszechÂświata niehomogenicznego i anizotropowego, ale — jak juÂż powyÂżej zaznaczono — taki to wÂłaÂśnie model jest logicznie konieczny[258], kiedy chcemy odpowiedzieĂŚ na pytanie o nie tylko przestrzenny, ale rĂłwnieÂż przestrzenno-czasowy charakter ksztaÂłtu Kosmosu. Kosmologia wspó³czesna zaÂś udzielaÂła — jak do tej pory — ‘wÂłaÂściwej odpowiedzi na niewÂłaÂściwe pytanie’. ByÂło tak zaÂś dlatego, poniewaÂż wspó³czeÂśnie nie umiemy z zasady — w przeciwieĂąstwie np. do staroÂżytnych GrekĂłw — myÂśleĂŚ posÂługujÂąc siĂŞ pojĂŞciami synkrytycznymi[259] — pojĂŞciami odnoszÂącym siĂŞ do jakichÂś obiektĂłw w ogĂłle, do rzeczy samych w sobie. Nie potrafimy obecnie juÂż mĂłwiĂŚ po prostu o „czymÂś”, a jedynie o „czymÂś jakimÂś”, o rzeczy w danym jej aspekcie. Nic zatem dziwnego, Âże i dzisiejszym fizykom zlewa siĂŞ pojĂŞcie „ksztaÂłtu WszechÂświata w ogĂłle” z jego bardziej szczegó³owÂą egzemplifikacjÂą — „ksztaÂłtu WszechÂświata w jego aspekcie ewolucyjnym, tj. dynamicznym, czyli wiĂŞc czasowym”. I tak o ile „WszechÂświat w ogĂłle” winien mieĂŚ (w pierwszym przybliÂżeniu) ksztaÂłt Parmenidejskiej kuli, o tyle WszechÂświat czasowy [universum obserwowane w czasie, a wiĂŞc universum w peÂłni fizykalne] jest hipertorusem rogowym. Jak widzimy, to wÂłaÂśnie zresztÂą model torusa rogowego wyjaÂśnia nam [na razie przynajmniej jakoÂściowo] wszystkie, pozornie jedynie sprzeczne, obserwacje dotyczÂące WszechÂświata[260].
OsobnÂą kwestiĂŞ stanowi tutaj problem szczegó³owego statusu geometrycznego omawianego przez nas modelu Kosmosu. Jak wiadomo, funkcjonujÂące dziÂś w tej materii modele opierajÂą swĂłj formalizm na geometrii rozmaitoÂści (ró¿niczkowalnych). Jak zauwaÂża jednak M. Heller: „KoniecznoœÌ odejÂścia od rozmaitoÂściowego modelu czasoprzestrzeni moÂże ujawniĂŚ siĂŞ w obszarze kwantowania grawitacji. IstniejÂą silne racje przemawiajÂące za tym, Âże skwantowanie pola grawitacyjnego — przede wszystkim na bardzo wczesnych etapach ewolucji WszechÂświata, w pobliÂżu tzw. poczÂątkowej osobliwoÂści — jest nie dajÂącÂą siĂŞ unikn¹Ì koniecznoÂściÂą. ChoĂŚ znane sÂą i inne propozycje, wysoce prawdopodobnym wydaje siĂŞ, Âże przy tego rodzaju zabiegu trzeba odstÂąpiĂŚ od rozmaitoÂściowej struktury czasoprzestrzeni. Zacytujmy na przykÂład opiniĂŞ Trautmana: ‘Topologiczne i ró¿niczkowe struktury czasoprzestrzeni nie wydajÂą siĂŞ posiadaĂŚ dobrze okreÂślonego operacyjnego znaczenia. Dlatego teÂż jest prawdopodobnym, Âże zostanÂą one porzucone, lub raczej zastÂąpione, przez jak¹œ innÂą strukturĂŞ, ktĂłra byÂłaby ÂściÂślej zwiÂązana z fizycznymi zjawiskami i ÂściÂślej przez nie wyznaczana niÂż absolutna, lokalnie euklidesowa struktura czasoprzestrzeni, zakÂładana we wszystkich obecnych teoriach. WedÂług mojej opinii, zadowalajÂąca kwantowa teoria przestrzeni, czasu i grawitacji bĂŞdzie musiaÂła odrzuciĂŚ pojĂŞcie rozmaitoÂści ró¿niczkowej jako modelu czasoprzestrzeni’ [...]”[261].
StrukturÂą, bĂŞdÂąca ‘ÂściÂślej zwiÂązanÂą z fizycznymi zjawiskami’ mogÂłaby byĂŚ [jak wynika juÂż z naszych dotychczasowych rozwaÂżaĂą] przestrzeĂą rozpinana przez [zawarty w niej] 2-wymiarowy, spiralny czas, naniesiony na ‘zÂłotÂą’, logarytmicznÂą spiralĂŞ, ktĂłrej kaÂżdy peÂłny obrĂłt kreowaÂłby kolejne — propagujÂące w postĂŞpie wÂłaÂśnie zÂłotym — pÂłaskie pentagonalne figury (pentagon, siatka dodekahedru etc.) [por. rys. 6]. Rzut spirali czasu na oÂś jednowymiarowÂą dawaÂłby czas liniowy skwantowany. PrzybliÂżyÂłoby to w istotny sposĂłb ‘unifikacjĂŞ’ czasu w dzisiejszej fizyce, ktĂłra dysponuje pĂłki co jedynie partykularnymi pojĂŞciami czasu: termodynamicznym, ‘grawitacyjnym’, kwantowym etc. Szczegó³owy formalizm takiej struktury wymagaÂłby dopiero opracowania. Jak zauwaÂża wszelako Ă. Klein: „KaÂżda z koncepcji fizycznych nadaje czasowi status oryginalny i szczegĂłlny. W rezultacie czas prezentuje zagadkowe oblicze sfinksa, jego istota zaÂś pozostaje mglista, nieokreÂślona i raczej niespĂłjna. Nie istnieje uniwersalna koncepcja czasu, nie ma wokó³ tego pojĂŞcia teoretycznej zgodnoÂści. [...]. Czy jednoœÌ czasu pojawiÂłaby siĂŞ, gdyby teoretycy zdoÂłali zunifikowaĂŚ cztery oddziaÂływania uznawane przez wspó³czesnÂą fizykĂŞ za podstawowe? A moÂże wrĂŞcz przeciwnie, brakuje im wÂłaÂśnie tej jednolitej wizji czasu, aby posun¹Ì do przodu sprawĂŞ unifikacji? Niewykluczone, Âże ró¿ne czasy [...] posiadajÂą jednak dobrze ukryte ‘twarde jÂądro’ wspĂłlnych wÂłasnoÂści. Wykazanie istnienia ‘zgodnoÂści czasĂłw’ w fizyce wprowadzaÂłoby porzÂądek tam, gdzie go bardzo brakuje, a ponadto rzuciÂłoby nowe ÂświatÂło na pewne nadal aktualne problemy podstawowe, jakie nastrĂŞcza na przykÂład interpretacja fizyki kwantowej. Z pytaĂą dotyczÂących natury czasu mogÂłyby siĂŞ wiĂŞc narodziĂŚ fundamentalne teorie jutra”[262].
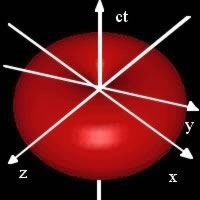
Rys. 15 Trudne do wizualizacji przedstawienie modelu Wszechœwiata w postaci 4-wymiarowego hipertoroidu rogowego, z czasem jako jego osi¹ symetrii. Nowego znaczenia nabiera tu znane [zw³aszcza wœród ziemskich biznesmenów] powiedzenie, ¿e wszystko w œwiecie krêci siê wokó³ czasu.
Czas waha siĂŞ tu cyklicznie w przedziale [-a, a], zaÂś dla r = a otrzymujemy punkty osobliwe (ewolucji) WszechÂświata. Od razu widaĂŚ, iÂż w tym modelu kaÂżde przemieszczenie [translacja] w przestrzeni jest zarazem podró¿¹ w czasie i vice versa. Kiedy siĂŞgamy w g³¹b przestrzeni, siĂŞgamy w g³¹b czasu — co jest zresztÂą doœÌ oczywiste — natomiast (jak juÂż wczeÂśniej zauwaÂżaliÂśmy) istnienie odlegÂłoÂści przestrzennej jest conditio sine qua non istnienia zjawisk czasowych. Poza tym WszechÂświat w tym modelu 'ekspanduje' — jak rĂłwnieÂż widaĂŚ — w tempie niejednostajnym i posiada 'momenty' osobliwe, co moÂże implikowaĂŚ niejednospĂłjnÂą topologiĂŞ. Model Ăłw wymaga teraz iloÂściowego sprawdzenia.
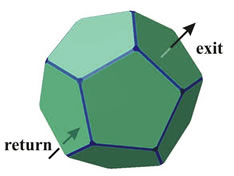
Rys. 16 NiejednospĂłjna topologia WszechÂświata jest wynikiem, logicznie rzecz biorÂąc, z jednej strony zamkniĂŞtoÂści, czyli teÂż peÂłni universum, z drugiej zaÂś moÂże byĂŚ zwiÂązana z przedstawionym powyÂżej zarysem cyklicznego modelu czasoprzestrzeni, w ktĂłrym czas jest okresowy i stanowi 'centrum' Kosmosu.
Konsekwencje adekwatnoÂści tegoÂż modelu byÂłyby m.in. nastĂŞpujÂące. Otó¿, jak wiadomo, trajektorie w przestrzeni fazowej systemu hamiltonowskiego, majÂącego n stopni swobody i posiadajÂącego n caÂłek ruchu, le¿¹ na n-wymiarowej rozmaitoÂści, ktĂłra jest topologicznie rĂłwnowaÂżna n-torusowi[267] [por. rys. 17]. Zatem WszechÂświat w ogĂłle, WszechÂświat jako caÂłoœÌ byÂłby adekwatnie opisywalny 'peÂłnym' torusem rogowym, zaÂś poszczegĂłlne czĂŞÂści ten WszechÂświat skÂładajÂące — w ogĂłlnoÂści 'niepeÂłnymi', wielowymiarowymi torusami (pierÂścieniowymi). To doskonaÂła ilustracja prawdy gÂłoszÂącej, Âże caÂłoœÌ jest czymÂś peÂłnym, to co ogĂłlne jest czymÂś prostym, a poszczegĂłlne skÂładniki tegoÂż ogó³u — niepeÂłne i skomplikowane.

Rys. 17 Orbity ciaÂł materialnych opisywanych w systemie hamiltonowskim (np. orbity planet) sytuujÂą siĂŞ na torusach fazowych (np. w przestrzeni zmiennych 'dziaÂłanie-kÂąt').
Warto tutaj w kaÂżdym razie jeszcze zaznaczyĂŚ, iÂż powiedzieliÂśmy powyÂżej rĂłwnieÂż coÂś nt. natury punktu poczÂątkowego — tj. wg np. OTW osobliwego punktu[268] — WszechÂświata. Nie zmienia to faktu, Âże posiadane dziÂś przez nas narzĂŞdzia teoretyczne nie sÂą w stanie dosiĂŞgn¹Ì opisu tego punktu, jednak — jak widaĂŚ — nawet juÂż prosta logika i rozum [a wiĂŞc 'narzĂŞdzia' doskonale znane juÂż Filolaosowi] sÂą zdolne wykroczyĂŚ — przynajmniej w sensie jakoÂściowym — poza najbardziej nawet dopracowane naukowe teorie
Jak pokazaliÂśmy do tej pory, nauka Filolaosa, niczym czerwona niĂŚ, przewija siĂŞ w toku dziejĂłw astronomii i kosmologii. Nazwisko pitagorejczyka, bÂądÂź jego uczniĂłw Archytasa oraz Platona, pojawia siĂŞ nader czĂŞsto tam, gdzie dokonane zostaje jakieÂś przeÂłomowe — i zdawaÂłoby siĂŞ caÂłkiem nowatorskie — odkrycie, dotyczÂące budowy oraz struktury Kosmosu, uÂświadamiajÂąc nam, Âże nie do koĂąca jest ono naprawdĂŞ nowatorskie. Co prawda usiÂłuje siĂŞ dziÂś przedstawiaĂŚ czĂŞsto poglÂądy antycznych uczonych jako archaiczne, a nawet logicznie niespĂłjnie, poglÂąd taki jednak — jak juÂż wyÂżej pokazaliÂśmy — sam jest logicznie niespĂłjny; toteÂż naleÂżaÂłoby go uznaĂŚ juÂż za archaiczny.
Zapewne takÂże „nie ma wÂątpliwoÂści”, iÂż czysto dedukcyjny system pitagorejsko-platoĂąski, wyprowadzajÂący swe tezy z najbardziej ogĂłlnych (synoptycznych), pierwotnych zasad (a. zasady) jest — logicznie rzecz biorÂąc — bardzo bliski juÂż na samym swym poczÂątku Teorii Wszystkiego, bÂądÂź wrĂŞcz stanowiĂŚ musi egzemplifikacjĂŞ takiej teorii. W dzisiejszej fizyce rozumuje siĂŞ zazwyczaj przez indukcjĂŞ i uogĂłlnianie — „od szczegó³ów do ogó³u”[280] — zatem najbardziej ogĂłlna teoria — Teoria Wszystkiego — jest w tym modelu myÂślenia dopiero finalnym, nieosiÂągalnym prawie punktem dojÂścia
Pitagorejskie twierdzenie, Âże ‘wszystko jest liczbÂą’ moÂże byĂŚ prawidÂłowo uzasadnialne logicznie. Liczba (naturalna) jest bowiem jednoÂściÂą wieloÂści (jednÂą wieloÂściÂą). Tymczasem wszystko, co nie jest wieloÂściÂą — jest jednoÂściÂą. To zaÂś, co nie jest wieloÂściÂą — musi byĂŚ jednoÂściÂą. Zatem nie moÂże istnieĂŚ nic, co nie byÂłoby ani wieloÂściÂą, ani jednoÂściÂą. Zarazem kaÂżda rzecz jest jednÂą i tÂą samÂą rzeczÂą [zasada toÂżsamoÂści].
PrzejdÂźmy teraz z kolei do bytĂłw „ponadprzestrzennych”. DoœÌ oczywistym jest, iÂż tak, jak ciaÂło geometryczne moÂżemy okreÂśliĂŚ za pomocÂą 3 wspó³rzĂŞdnych (dÂługoœÌ, szerokoœÌ, wysokoœÌ), tak „ciaÂło o wÂłasnoÂściach fizycznych” („posiadajÂące barwĂŞ”, czyli pewnie po prostu jak¹œ konsystencjĂŞ, a. ogĂłlniej — stan skupienia) da siĂŞ opisaĂŚ za pomocÂą tych trzech oraz jeszcze jednej wspó³rzĂŞdnej, oznaczajÂącej masĂŞ. Innymi sÂłowy kaÂżdy punkt bryÂły geometrycznej, jako obciĂŞcia 3-wymiarowej przestrzeni, jest caÂłkowicie okreÂślony trzema liczbami, zaÂś kaÂżdy odnoÂśny punkt jako czêœÌ ciaÂła fizycznego — czterema liczbami, z ktĂłrych czwarta oznacza masĂŞ skupionÂą w danej, infinitezymalnej czĂŞÂści 3-wymiarowego ksztaÂłtu ciaÂła. Tak samo zatem, jak ciaÂło geometryczne mogliÂśmy potraktowaĂŚ jako swego rodzaju ciÂąg (a. continuum) pÂłaszczyzn, tak i ciaÂło fizyczne (masywne) moÂżemy potraktowaĂŚ jako ciÂąg (a. continuum) geometrycznych bryÂł, lub teÂż jako geometrycznÂą bry³ê, ktĂłrej przypiszemy jeszcze w kaÂżdym jej punkcie czwartÂą wspó³rzĂŞdnÂą — masĂŞ.
PodstawÂą naszego poznania jest ujĂŞcie, tzn. objĂŞcie rzeczy(-wistoÂści), czyli forma (to, co ogranicza)[333]. MoÂżemy ten aspekt WszechÂświata nazwaĂŚ takÂże jego (zewnĂŞtrznym) obliczem (physis). ZajmowaĂŚ siĂŞ nim powinna (szeroko rozumiana) fizyka, jako nauka nie tylko o materialnym aspekcie Âświata, ale o wszystkich aspektach formalnych tegoÂż Âświata.
ÂŁatwo jest pokazaĂŚ, Âże pitagorejsko-platoĂąski paradygmat nauki — taki, jakim go w nin. pracy zrekonstruowaliÂśmy — prowadzi wprost i natychmiast do skonstruowania (czy teÂż moÂże raczej: odkrycia) wci¹¿ nieosiÂągalnego w dzisiejszej fizyce szczytu i zwieĂączenia tejÂże fizyki, jakim byÂłaby dla niej bÂądÂź tzw. jednolita teoria pola, tj. „ogĂłlna teoria, ktĂłra powiÂązaÂłaby oddziaÂływania elektromagnetyczne, grawitacyjne, silne i sÂłabe jednym ukÂładem rĂłwnaĂą”[335], bÂądÂź takÂże tzw. teoria wszystkiego, tj. „teoria, ktĂłra podaje jednolity opis wszystkich znanych typĂłw czÂąstek elementarnych, wszystkich znanych rodzajĂłw siÂł we WszechÂświecie oraz ewolucji WszechÂświata”
ZakoĂączenie
I tak oto doszliœmy do koùca naszych rozwa¿aù. Dotyczy³y one w istocie zagadnienia mitu liniowego postêpu nauki. Jak okaza³o siê powy¿ej, pomimo i¿ mit ten (jak zreszt¹ na ogó³ wszystkie mity) ma szeroki zakres i du¿¹ si³ê oddzia³ywania, jest jednak z punktu widzenia faktów nazbyt dos³ownie interpretowany i przyjmowany. Niew¹tpliwie tkwi¹ w nim ziarna prawdy w tym sensie, ¿e nauka nowo¿ytna dokonuje bezustannego iloœciowego postêpu wiedzy. Ale twierdzenie, ¿e istnieje dziœ równie¿ sta³y postêp w metodzie myœlenia, w dokonywaniu wgl¹du w rzeczywistoœÌ i w metodologicznej analizie odkrywanych naukowych teorii budzi ju¿ znaczn¹ w¹tpliwoœÌ.
PosÂługujÂąc siĂŞ metodami ÂścisÂłego (choĂŚ zarazem bardzo abstrakcyjnego) logicznego myÂślenia, jakie byÂły juÂż znane staroÂżytnym, moÂżemy nie tylko zrozumieĂŚ gÂłeboko sens odkrywanych dziÂś przez nas w fizyce i astronomii empirycznych faktĂłw i uzyskaĂŚ w nie wglÂąd; moÂżemy rĂłwnieÂż przewidywaĂŚ nowe, przyszÂłe odkrycia (jak odkrycie, nie powstaÂłej jeszcze do dzisiaj, OgĂłlnej Teorii Pola).
Konkluzje te mogÂą nas niepokoiĂŚ. SÂą one bowiem obligatoryjne. PrzyjÂąwszy je jako prawdĂŞ, nie moÂżemy nie staraĂŚ siĂŞ zmieniĂŚ podejÂścia do odkrywania Prawdy naukowej. W szczegĂłlnoÂści nie moÂżemy w takim razie zatrzymywaĂŚ siĂŞ na zdroworozsÂądkowym etapie poznania rzeczywistoÂści i twierdziĂŚ nadal, Âże jest to etap najwyÂższy. ÂŚwiadomoœÌ, Âże poza metodÂą nauk empirycznych istnieje jeszcze coÂś wiĂŞcej jest z pewnoÂściÂą bardzo niewygodna, zmusza do najwyÂższych umysÂłowych oraz duchowych wysiÂłkĂłw. Dlatego teÂż naukowcy przez setki lat — poczynajÂąc od Ăłwczesnych krytykĂłw Kopernika, Galileusza i Newtona (a nawet jeszcze wczeÂśniej) bronili siĂŞ przed tÂą ÂświadomoÂściÂą i bĂŞdÂą jÂą z ca³¹ pewnoÂściÂą dalej odrzucaĂŚ.
http://www.gnosis.art.pl/e_gnosis/aurea_catena_gnosis/zawisza_czerwona_nic/zawisza_czerwona_nic06.htm